플로이드 워셜
플로이드 워셜은 다익스트라와 마찬가지로 최단 경로를 구하는 알고리즘입니다.
1. 다익스트라와 플로이드 워셜
다익스트라와의 큰 차이점은 플로이드 워셜은 모든 노드에서 도착할 수 있는 모든 노드의 최소거리를 구하는 알고리즘, 다익스트라는 특정 노드에서 이동할 수 있는 모든 노드에 대해 최소거리를 구하는 알고리즘입니다. (다익스트라는 양의 가중치만 허용됩니다)
- 즉, 다익스트라는 부산에서 서울 대구까지의 최소 거리를 구하는 알고리즘이고
- 플로이드 워셜은 부산-대구, 부산-서울, 서울-대구의 거리를 한 번에 계산합니다
2. 플로이드 워셜 점화식
모든 노드별로 특정 노드를 거쳐 다른 노드로 가는 최단 경로를 저장하기 위해 2차원 LIST를 사용합니다. 따라서 전체 노드가 N개일 때, 알고리즘의 시간 복잡도는 O(N^3)입니다. 때문에 모드의 개수가 적다면 플로이드 워셜을 활용하는 것이 효과적이지만... 많을 때는 다익스트라 알고리즘을 사용하는 것이 효과적입니다.
플로이드 워셜의 점화식은 아래와 같습니다.
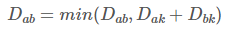
- D(ab)는 노드 A에서 B로 가는 최단 거리를 의미합니다.
- 위 식은 A에서 B로가는 최단거리와 A에서 K를 거쳐 B로가는 거리 중 최단 거리로 갱신하라는 것입니다.
3. 동작과정
우선, 자기 자신으로 가는 값은 0 이므로 대각선 값은 모두 0으로 만들어 줍니다.
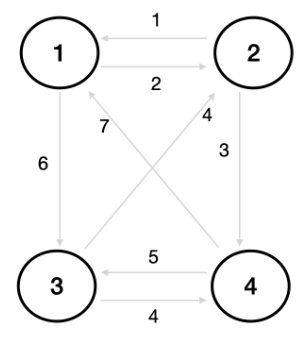
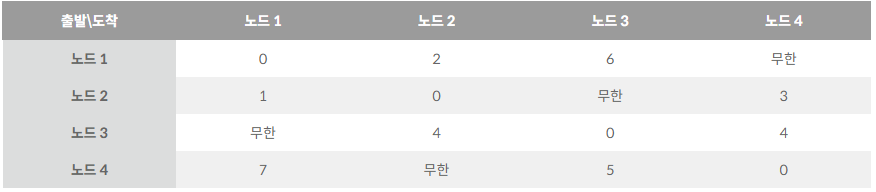
- 대각선은 0으로 초기화하고 나머지는 INF(1e9)로 나둡니다.
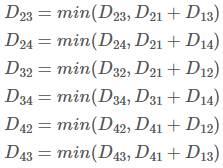
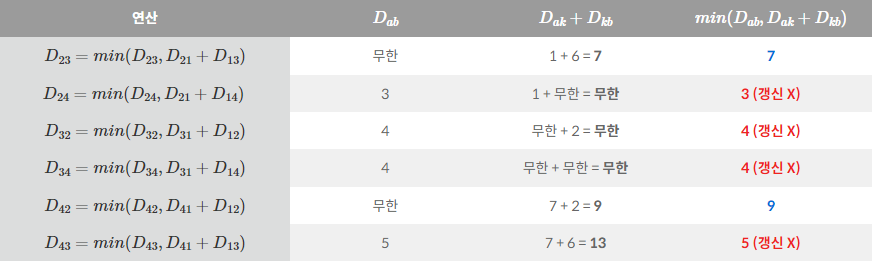
- 1번 노드를 거쳐 다른 노드로 가는 최단 거리를 계산합니다.
- 위 연산을 통해 갱신된 노드는 파란색, 갱신되지 않은 노드는 빨간색으로 표하겠습니다.
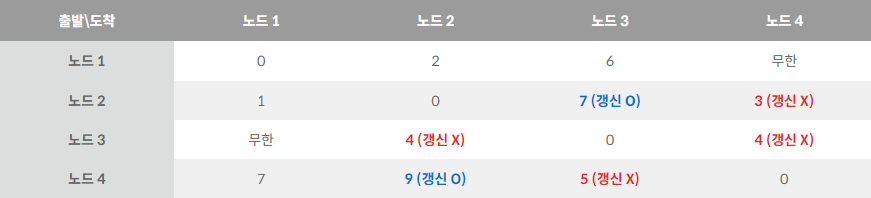
- 최종적으로 최단 거리 테이블은 아래와 같게 됩니다.
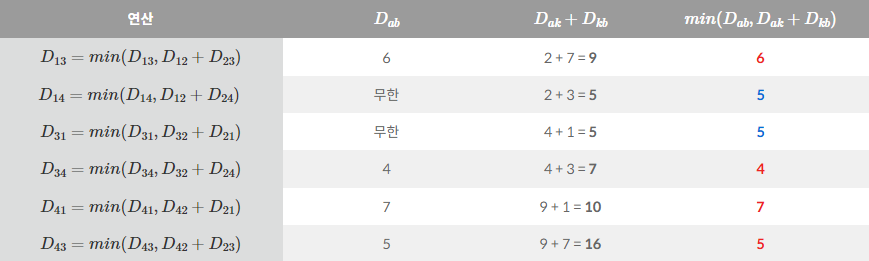
- 다음은 2번 노드를 거쳐 다른 노드로 가는 최단 거리를 계산합니다.
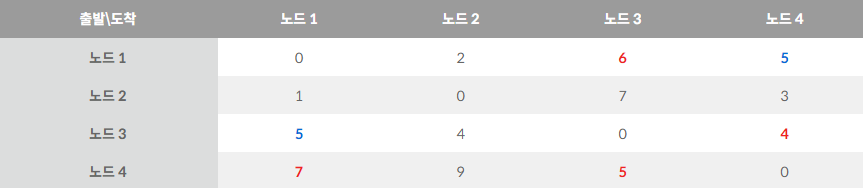
- 전체 노드를 이와 같은 방법으로 해주면 결과적으로 나오는 테이블은 아래와 같습니다.
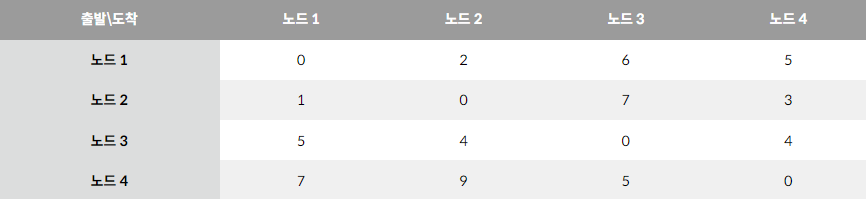
- 문제 적용은 다음 문단에서 해봅시다.
4. 문제 설명
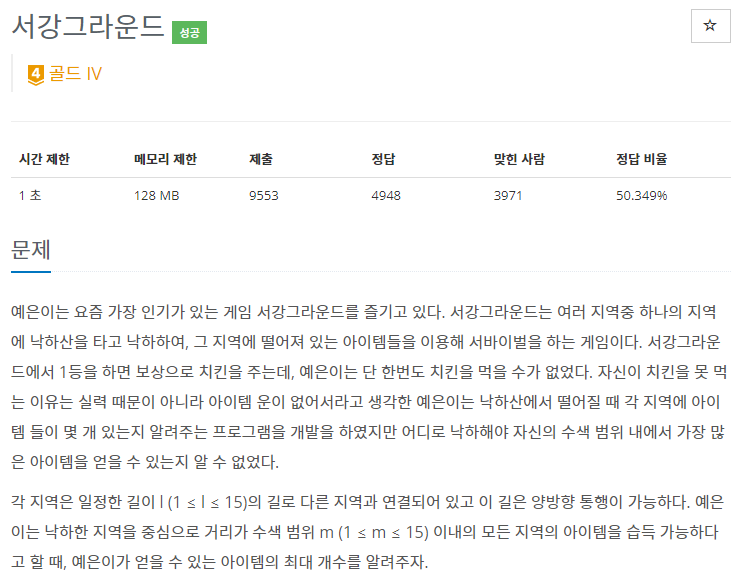
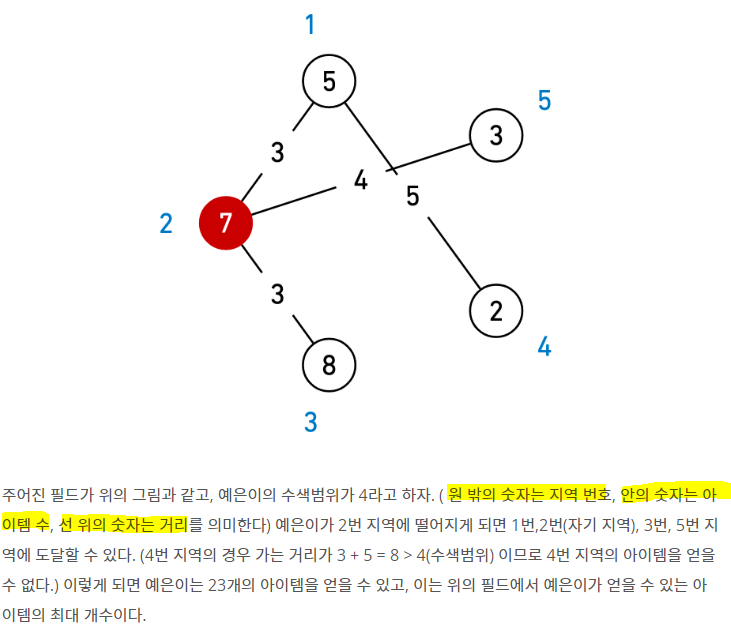
- 요약하면 예은이는 4만큼 움직일 수 있다. 즉 2번 지역에 떨어지면 4번 지역을 제외한 모든 구역에 방문이 가능하다. 그렇다면 7 + 5 + 3 + 8 = 23 총 23개의 아이템을 얻어 가장 많은 아이템을 얻을 수 있는 경우가 된다.
늘 이야기하지만 문제를 이해하는 게 1순위 같습니다. 늘 이야기한 적은 없지만.
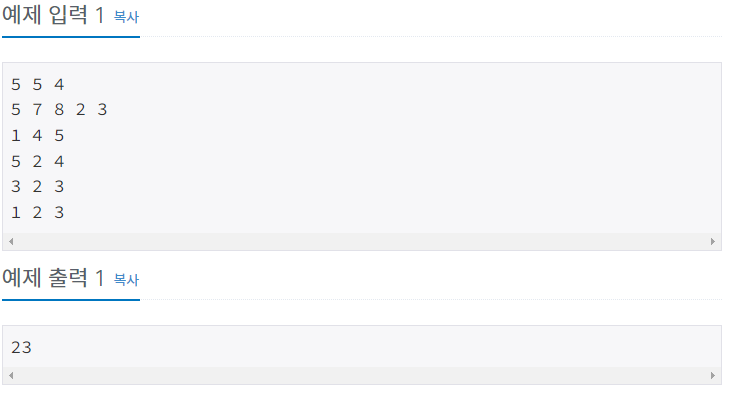
- 이문제를 살펴봅시다. 우선 모든 지역에서 얻을 수 있는 아이템수를 조사해야 합니다.
특정 지역이 아닌 모든 지역이라는 점에서 플로이드 워셜을 생각할 수 있습니다. 또한 플로이드 워셜은 시간 복잡도가 O(N^3)입니다. 노드 수는 100개 이하로 주어집니다. 최악의 경우는 100^3 즉 1000000, 100만입니다. 충분히 해볼 만합니다. python은 1초에 2000만 번의 연산이 가능하기 때문이죠.
자 그러면 '플로이드 워셜을 써야겠다'라는 결론이 나옵니다.
INF = int(1e9)
N, M, R = map(int, input().split())
item = list(map(int, input().split()))
visited = [[INF] * N for _ in range(N)]
MAX = 0
- 먼저 input을 받아줍니다. N은 지역의 수(노드 수), M은 예은이의 활동범위, R은 길의 수(간선의 개수)입니다.
둘째 줄에는 각구역에 아이템 수를 알려주고
셋째 줄부터는 시작지역, 도착지역, 길의 길이 순서로 주어진다.
for _ in range(R):
s, e, d = map(int, input().split())
visited[s-1][e-1] = min(visited[s-1][e-1], d)
visited[e-1][s-1] = min(visited[e-1][s-1], d)
- 저는 거리를 갱신해 줄 테이블을 visited라고 지었습니다. 모든 원소는 INF(1e9)로 넣어주고 2차원 리스트로 생성했고, 주어진 지역의 번호는 1부터 시작하기 때문에 저는 0부터 시작을 하려고 s-1, e-1을 해주었습니다. 또한 그 인덱스의 원소값을 d로 초기화했습니다.
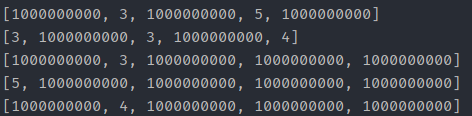
- 그 결과 위와 같은 테이블이 완성됩니다.
- 그리고 플로이드 워셜이 나오게 됩니다.
for i in range(N):
for j in range(N):
for k in range(N):
visited[j][k] = min(visited[j][k], visited[j][i] + visited[i][k])
if j == k:
visited[j][k] = False
- 순서대로 경 출 도 (경유지, 출발지, 도착지)라 외웁시다. 그냥 외웁시다.
- 위쪽에서 점화식을 알려 드렸습니다. 그와 같이 적으면 됩니다. 또한 저는 이 시점에서 대각선 원소들을 False 값으로 설정했습니다.
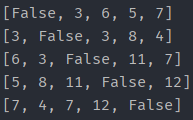
- 이 과정을 거쳐 테이블이 완성되었고 이는 거리를 의미합니다. 그럼 그 값이 M 보다 작은 곳의 아이템을 모조리 가져오면 됩니다.
for i in range(N):
cnt = 0
for j in range(N):
if visited[i][j] <= M:
cnt += item[j]
MAX = max(MAX, cnt)
print(MAX)
- 2중 for문을 통해 거리를 판단하고 그 거리가 M보다 작거나 같을 때 item list의 [j] 번째 원소를 cnt에 더해줍니다. 그리고 MAX 값과 비교해 큰 값으로 갱신해 주면 결국 MAX에는 가장 많은 아이템을 얻었을 때 값이 들어가게 됩니다.
5. 전체 코드
INF = int(1e9)
N, M, R = map(int, input().split())
item = list(map(int, input().split()))
visited = [[INF] * N for _ in range(N)]
MAX = 0
for _ in range(R):
s, e, d = map(int, input().split())
visited[s-1][e-1] = min(visited[s-1][e-1], d)
visited[e-1][s-1] = min(visited[e-1][s-1], d)
for i in range(N):
for j in range(N):
for k in range(N):
visited[j][k] = min(visited[j][k], visited[j][i] + visited[i][k])
if j == k:
visited[j][k] = False
for i in range(N):
cnt = 0
for j in range(N):
if visited[i][j] <= M:
cnt += item[j]
MAX = max(MAX, cnt)
print(MAX)6. 후기
처음이 어렵습니다. 뭐라는지...
그래도 다익스트라를 하고 와서 그런지 이해가 수월했습니다.
이 문제 같은 경우는 2차원 리스트를 어떻게 사용할지를 차근차근 이해하면 쉬웠습니다.
또한 경 출 도 만 외우면 플로이드는 쉽게 사용할 수 있을 것 같다. 아! 점화식도 포함..
이상 플로이드 였습니다.
'알고리즘 > python' 카테고리의 다른 글
| [프로그래머스] lv2 타겟 넘버_python (0) | 2024.03.22 |
|---|---|
| [BOJ]ACM Craft(1005), 위상정렬 (0) | 2023.04.19 |
| [BOJ]N-QUEEN(9663), 백트래킹 (2) | 2023.04.19 |
| [SWEA] 16940. 퀵 정렬 (0) | 2023.04.19 |
| [BOJ]문자열 게임(18241), 문자열 (0) | 2023.04.19 |
플로이드 워셜
플로이드 워셜은 다익스트라와 마찬가지로 최단 경로를 구하는 알고리즘입니다.

1. 다익스트라와 플로이드 워셜
다익스트라와의 큰 차이점은 플로이드 워셜은 모든 노드에서 도착할 수 있는 모든 노드의 최소거리를 구하는 알고리즘, 다익스트라는 특정 노드에서 이동할 수 있는 모든 노드에 대해 최소거리를 구하는 알고리즘입니다. (다익스트라는 양의 가중치만 허용됩니다)
- 즉, 다익스트라는 부산에서 서울 대구까지의 최소 거리를 구하는 알고리즘이고
- 플로이드 워셜은 부산-대구, 부산-서울, 서울-대구의 거리를 한 번에 계산합니다
2. 플로이드 워셜 점화식
모든 노드별로 특정 노드를 거쳐 다른 노드로 가는 최단 경로를 저장하기 위해 2차원 LIST를 사용합니다. 따라서 전체 노드가 N개일 때, 알고리즘의 시간 복잡도는 O(N^3)입니다. 때문에 모드의 개수가 적다면 플로이드 워셜을 활용하는 것이 효과적이지만... 많을 때는 다익스트라 알고리즘을 사용하는 것이 효과적입니다.
플로이드 워셜의 점화식은 아래와 같습니다.
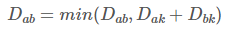
- D(ab)는 노드 A에서 B로 가는 최단 거리를 의미합니다.
- 위 식은 A에서 B로가는 최단거리와 A에서 K를 거쳐 B로가는 거리 중 최단 거리로 갱신하라는 것입니다.
3. 동작과정
우선, 자기 자신으로 가는 값은 0 이므로 대각선 값은 모두 0으로 만들어 줍니다.


- 대각선은 0으로 초기화하고 나머지는 INF(1e9)로 나둡니다.
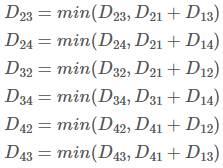
- 1번 노드를 거쳐 다른 노드로 가는 최단 거리를 계산합니다.
- 위 연산을 통해 갱신된 노드는 파란색, 갱신되지 않은 노드는 빨간색으로 표하겠습니다.

- 최종적으로 최단 거리 테이블은 아래와 같게 됩니다.

- 다음은 2번 노드를 거쳐 다른 노드로 가는 최단 거리를 계산합니다.


- 전체 노드를 이와 같은 방법으로 해주면 결과적으로 나오는 테이블은 아래와 같습니다.

- 문제 적용은 다음 문단에서 해봅시다.
4. 문제 설명


- 요약하면 예은이는 4만큼 움직일 수 있다. 즉 2번 지역에 떨어지면 4번 지역을 제외한 모든 구역에 방문이 가능하다. 그렇다면 7 + 5 + 3 + 8 = 23 총 23개의 아이템을 얻어 가장 많은 아이템을 얻을 수 있는 경우가 된다.
늘 이야기하지만 문제를 이해하는 게 1순위 같습니다. 늘 이야기한 적은 없지만.

- 이문제를 살펴봅시다. 우선 모든 지역에서 얻을 수 있는 아이템수를 조사해야 합니다.
특정 지역이 아닌 모든 지역이라는 점에서 플로이드 워셜을 생각할 수 있습니다. 또한 플로이드 워셜은 시간 복잡도가 O(N^3)입니다. 노드 수는 100개 이하로 주어집니다. 최악의 경우는 100^3 즉 1000000, 100만입니다. 충분히 해볼 만합니다. python은 1초에 2000만 번의 연산이 가능하기 때문이죠.
자 그러면 '플로이드 워셜을 써야겠다'라는 결론이 나옵니다.
INF = int(1e9)
N, M, R = map(int, input().split())
item = list(map(int, input().split()))
visited = [[INF] * N for _ in range(N)]
MAX = 0
- 먼저 input을 받아줍니다. N은 지역의 수(노드 수), M은 예은이의 활동범위, R은 길의 수(간선의 개수)입니다.
둘째 줄에는 각구역에 아이템 수를 알려주고
셋째 줄부터는 시작지역, 도착지역, 길의 길이 순서로 주어진다.
for _ in range(R):
s, e, d = map(int, input().split())
visited[s-1][e-1] = min(visited[s-1][e-1], d)
visited[e-1][s-1] = min(visited[e-1][s-1], d)
- 저는 거리를 갱신해 줄 테이블을 visited라고 지었습니다. 모든 원소는 INF(1e9)로 넣어주고 2차원 리스트로 생성했고, 주어진 지역의 번호는 1부터 시작하기 때문에 저는 0부터 시작을 하려고 s-1, e-1을 해주었습니다. 또한 그 인덱스의 원소값을 d로 초기화했습니다.

- 그 결과 위와 같은 테이블이 완성됩니다.
- 그리고 플로이드 워셜이 나오게 됩니다.
for i in range(N):
for j in range(N):
for k in range(N):
visited[j][k] = min(visited[j][k], visited[j][i] + visited[i][k])
if j == k:
visited[j][k] = False
- 순서대로 경 출 도 (경유지, 출발지, 도착지)라 외웁시다. 그냥 외웁시다.
- 위쪽에서 점화식을 알려 드렸습니다. 그와 같이 적으면 됩니다. 또한 저는 이 시점에서 대각선 원소들을 False 값으로 설정했습니다.

- 이 과정을 거쳐 테이블이 완성되었고 이는 거리를 의미합니다. 그럼 그 값이 M 보다 작은 곳의 아이템을 모조리 가져오면 됩니다.
for i in range(N):
cnt = 0
for j in range(N):
if visited[i][j] <= M:
cnt += item[j]
MAX = max(MAX, cnt)
print(MAX)
- 2중 for문을 통해 거리를 판단하고 그 거리가 M보다 작거나 같을 때 item list의 [j] 번째 원소를 cnt에 더해줍니다. 그리고 MAX 값과 비교해 큰 값으로 갱신해 주면 결국 MAX에는 가장 많은 아이템을 얻었을 때 값이 들어가게 됩니다.
5. 전체 코드
INF = int(1e9)
N, M, R = map(int, input().split())
item = list(map(int, input().split()))
visited = [[INF] * N for _ in range(N)]
MAX = 0
for _ in range(R):
s, e, d = map(int, input().split())
visited[s-1][e-1] = min(visited[s-1][e-1], d)
visited[e-1][s-1] = min(visited[e-1][s-1], d)
for i in range(N):
for j in range(N):
for k in range(N):
visited[j][k] = min(visited[j][k], visited[j][i] + visited[i][k])
if j == k:
visited[j][k] = False
for i in range(N):
cnt = 0
for j in range(N):
if visited[i][j] <= M:
cnt += item[j]
MAX = max(MAX, cnt)
print(MAX)6. 후기
처음이 어렵습니다. 뭐라는지...
그래도 다익스트라를 하고 와서 그런지 이해가 수월했습니다.
이 문제 같은 경우는 2차원 리스트를 어떻게 사용할지를 차근차근 이해하면 쉬웠습니다.
또한 경 출 도 만 외우면 플로이드는 쉽게 사용할 수 있을 것 같다. 아! 점화식도 포함..
이상 플로이드 였습니다.
'알고리즘 > python' 카테고리의 다른 글
| [프로그래머스] lv2 타겟 넘버_python (0) | 2024.03.22 |
|---|---|
| [BOJ]ACM Craft(1005), 위상정렬 (0) | 2023.04.19 |
| [BOJ]N-QUEEN(9663), 백트래킹 (2) | 2023.04.19 |
| [SWEA] 16940. 퀵 정렬 (0) | 2023.04.19 |
| [BOJ]문자열 게임(18241), 문자열 (0) | 2023.04.19 |
