728x90
반응형
백트래킹
단어 그대로 자식 노드의 유망성을 판단한 뒤 해당 노드가 유망하지 않다면 부모 노드로 돌아가 다른 자식 노드를 찾는 방법이다.
1. DFS와 백트래킹
그래프 탐색 기법 중 하나인 DFS와 백트레킹의 차이를 먼저 알아보기 위해 예시를 한번 보자.
- 0 <= a, b, c, d <= 100
- a+b+c+d = 30 이 되는 a, b, c, d를 모두 구하여라.
- a = 10이라도 b = 0 ~ 100, c = 0 ~ 100, d = 0 ~ 100 이 될 수 있다.
- 만약 a = 10 이라면 b는 0 <= b <= 20 이 된다.
- 이러한 모든 경우의 수를 찾아서 탐색하는 것이 DFS이다.
백트레킹의 경우를 찾아보자. - 이 경우 0부터 시작해서 모든 조합을 찾아나갈 것이다.
- b = 21이라면 그 이상은 탐색할 필요가 없어지게 되고 다음으로
- a = 11 일 때 b, c, d의 경우를 찾는 절차를 밟게 된다.
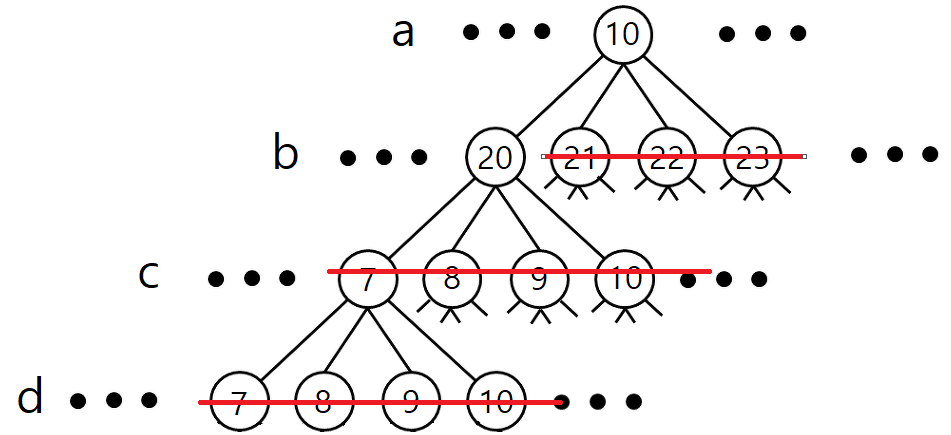
백트레킹은 이와 같이 유망하지 않은 노드의 경우 탐색을 중단하고 부모노드로 되돌아가게 된다.
정리하자면 다음과 같다.
- 백트레킹은 탐색가능한 모든 경우의 수 중 특정 조건을 만족하는 수만 탐색하는 것이다.
- 즉 답이 될만한지 판단하고 그렇지 않을 경우 유망하지 않은 경우 가지치기를 하는 것이다.
- 백트레킹 문제는 DFS의 과정에서 조건을 주며 절대 답이 되지 않을 상황을 정의하고, 그 상황의 경우 탐색을 중단하고 다시 부모 노드로 돌아가 다른 경우를 탐색하게 끔 한다.
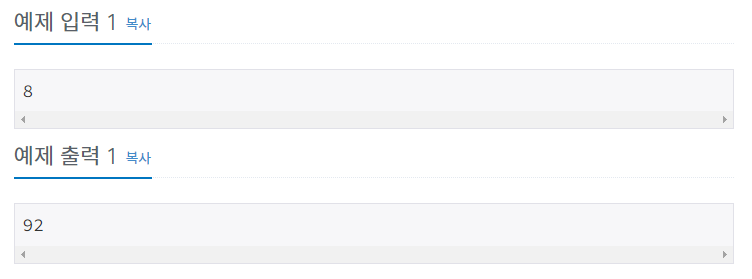
- 퀸은 아래와 같이 움직인다.
- 말 그대로 N×N 체스판에서 N개의 퀸이 서로 공격할 수 없게 놓는 것이다.
2. 문제 설명
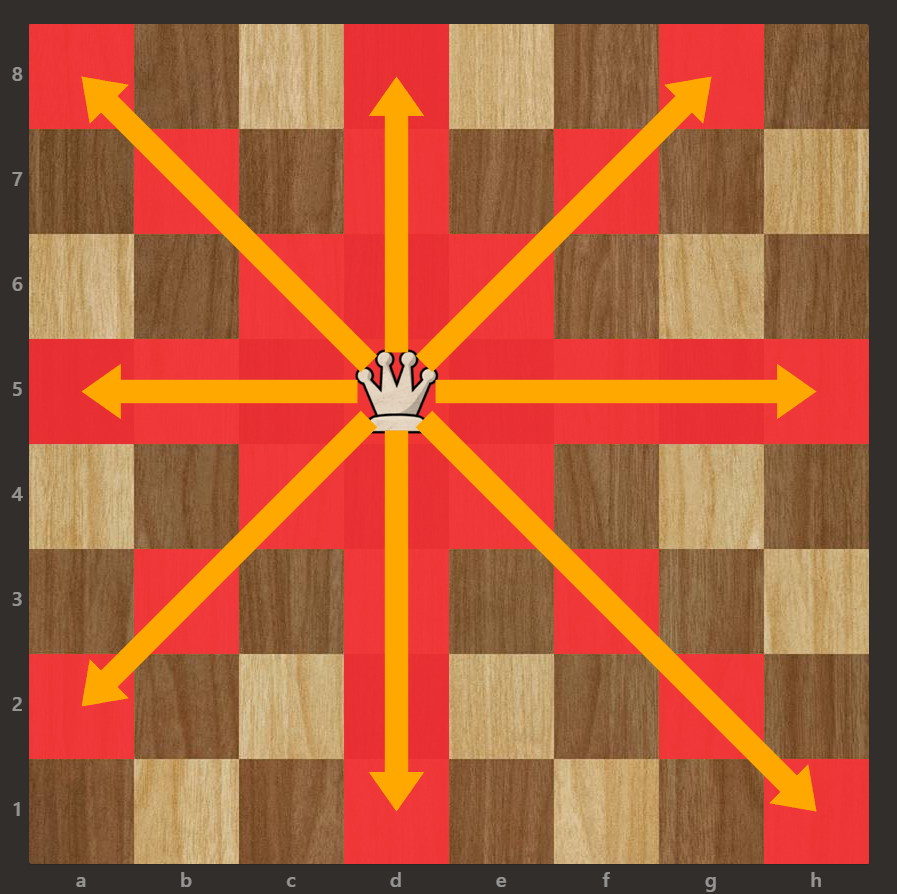
3. 문제 풀이
- 예시로 아래는 4 ×4 체스판에 퀸 4개가 공격할 수 없게 놔두는 경우의 하나이다.
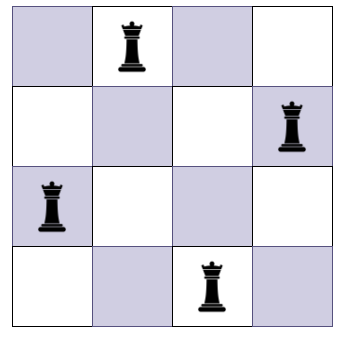
- 가장 좌측열에서 부터 하나씩 비교하며 해당 열의 모든 행에 퀸이 있는지 확인한다.
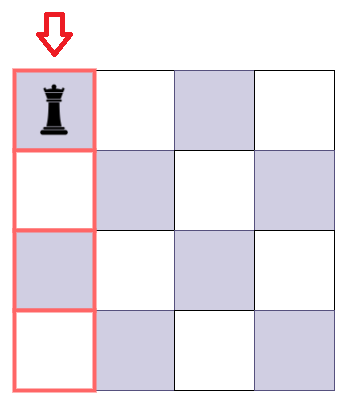
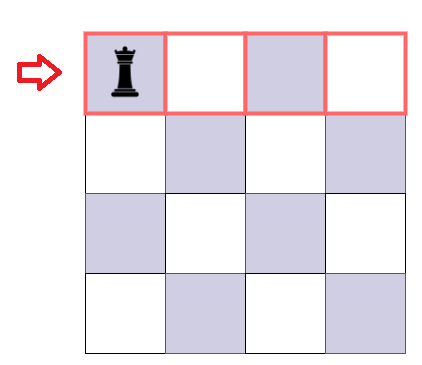
- 각 행을 체크할 때, 퀸이 없다면 유망한 후보로 고르고 해당 행 전체에 퀸이 있는지 조사한다.
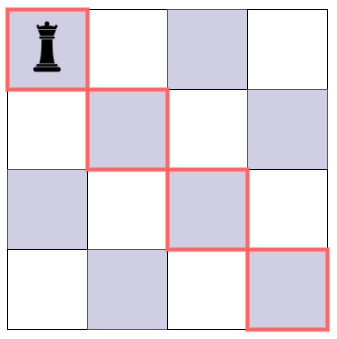
- 이 또한 체크되었다면, 대각선을 확인한다.
- 이 과정을 통해 3행까지 확인이 된다면 다음 퀸은 3행 2열에 배치될 것이다.
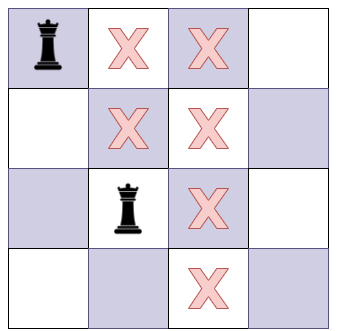
- 하지만 이 경우 다음은 어떠한 곳도 퀸을 배치할 수 없다. 그렇다면 다시 2행으로 돌아가 다른 곳에 배치하게 될 것이다.
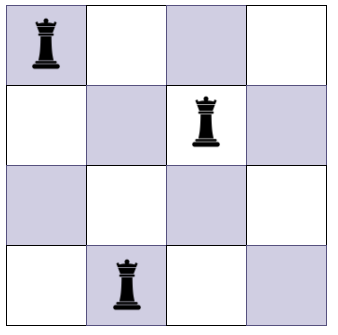
- 이 경우도 놓을 수 없으므로 1행으로 돌아가 다시 퀸을 배치하게 된다.
- 이 과정을 반복할 경우 완성되는 체스판은 아래와 같게 된다.
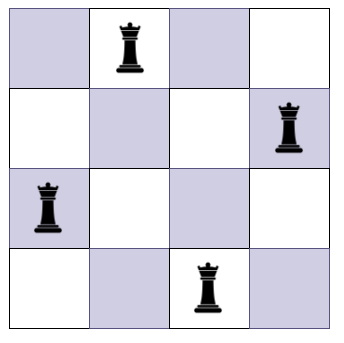
4. 코드
import sys
input = sys.stdin.readline
def is_promising(S):
for i in range(S):
# 같은 열과 행에 있으면 안되고, # 대각선에 있으면 안되며, 1칸 차이가 나도 안된다.
if l[S] == l[i] or abs(l[S]-l[i]) == S-i:
return False
return True
def Queen(S):
global ans
if S == N: # 끝줄까지 탐색 했으면
ans += 1
else:
for i in range(N):
l[S] = i
if is_promising(S):
Queen(S+1)
N = int(input())
ans = 0
l = [0]*N
Queen(0)
print(ans)5. 후기
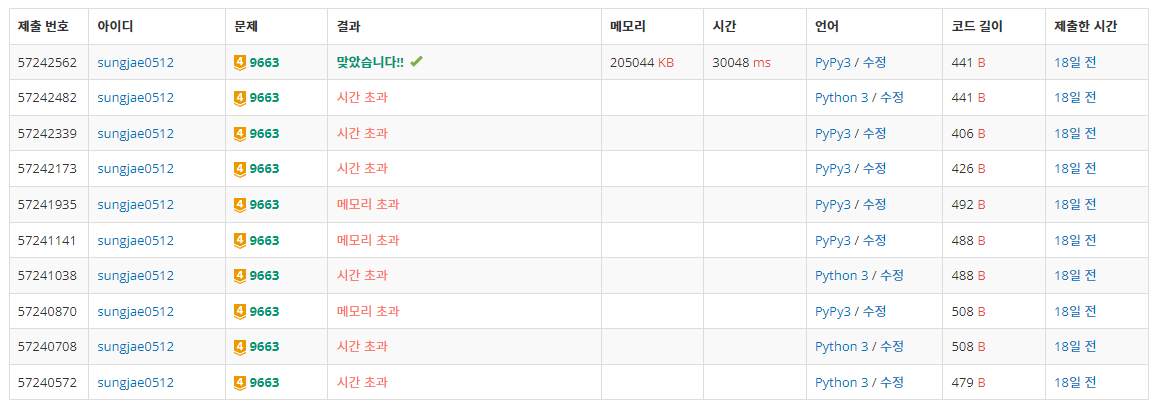
- 이 문제.. 백트레킹의 정석 문제라고 불린다. 난 이 문제를 풀며 상당한 고통을 느꼈다. 여러 번의 최적화 끝에 조건문을 간단히 작성하여 is_promising 함수를 완성했다.
백트레킹은 여러 방법이 있는 것 같다. 다른 문제를 풀다 보니
DFS에 백트레킹이 있는 것이 아니라 백트레킹 안에 DFS가 있는 느낌이다.
728x90
반응형
'알고리즘 > python' 카테고리의 다른 글
| [BOJ]ACM Craft(1005), 위상정렬 (0) | 2023.04.19 |
|---|---|
| [BOJ]서강그라운드(14938), 플로이드-워셜 (0) | 2023.04.19 |
| [SWEA] 16940. 퀵 정렬 (0) | 2023.04.19 |
| [BOJ]문자열 게임(18241), 문자열 (0) | 2023.04.19 |
| [BOJ]최소비용 구하기(1916), 다익스트라 (0) | 2023.04.19 |
728x90
반응형
백트래킹
단어 그대로 자식 노드의 유망성을 판단한 뒤 해당 노드가 유망하지 않다면 부모 노드로 돌아가 다른 자식 노드를 찾는 방법이다.
1. DFS와 백트래킹
그래프 탐색 기법 중 하나인 DFS와 백트레킹의 차이를 먼저 알아보기 위해 예시를 한번 보자.
- 0 <= a, b, c, d <= 100
- a+b+c+d = 30 이 되는 a, b, c, d를 모두 구하여라.
- a = 10이라도 b = 0 ~ 100, c = 0 ~ 100, d = 0 ~ 100 이 될 수 있다.
- 만약 a = 10 이라면 b는 0 <= b <= 20 이 된다.
- 이러한 모든 경우의 수를 찾아서 탐색하는 것이 DFS이다.
백트레킹의 경우를 찾아보자. - 이 경우 0부터 시작해서 모든 조합을 찾아나갈 것이다.
- b = 21이라면 그 이상은 탐색할 필요가 없어지게 되고 다음으로
- a = 11 일 때 b, c, d의 경우를 찾는 절차를 밟게 된다.

백트레킹은 이와 같이 유망하지 않은 노드의 경우 탐색을 중단하고 부모노드로 되돌아가게 된다.
정리하자면 다음과 같다.
- 백트레킹은 탐색가능한 모든 경우의 수 중 특정 조건을 만족하는 수만 탐색하는 것이다.
- 즉 답이 될만한지 판단하고 그렇지 않을 경우 유망하지 않은 경우 가지치기를 하는 것이다.
- 백트레킹 문제는 DFS의 과정에서 조건을 주며 절대 답이 되지 않을 상황을 정의하고, 그 상황의 경우 탐색을 중단하고 다시 부모 노드로 돌아가 다른 경우를 탐색하게 끔 한다.

- 퀸은 아래와 같이 움직인다.
- 말 그대로 N×N 체스판에서 N개의 퀸이 서로 공격할 수 없게 놓는 것이다.
2. 문제 설명


3. 문제 풀이
- 예시로 아래는 4 ×4 체스판에 퀸 4개가 공격할 수 없게 놔두는 경우의 하나이다.

- 가장 좌측열에서 부터 하나씩 비교하며 해당 열의 모든 행에 퀸이 있는지 확인한다.

- 각 행을 체크할 때, 퀸이 없다면 유망한 후보로 고르고 해당 행 전체에 퀸이 있는지 조사한다.

- 이 또한 체크되었다면, 대각선을 확인한다.

- 이 과정을 통해 3행까지 확인이 된다면 다음 퀸은 3행 2열에 배치될 것이다.

- 하지만 이 경우 다음은 어떠한 곳도 퀸을 배치할 수 없다. 그렇다면 다시 2행으로 돌아가 다른 곳에 배치하게 될 것이다.

- 이 경우도 놓을 수 없으므로 1행으로 돌아가 다시 퀸을 배치하게 된다.
- 이 과정을 반복할 경우 완성되는 체스판은 아래와 같게 된다.

4. 코드
import sys
input = sys.stdin.readline
def is_promising(S):
for i in range(S):
# 같은 열과 행에 있으면 안되고, # 대각선에 있으면 안되며, 1칸 차이가 나도 안된다.
if l[S] == l[i] or abs(l[S]-l[i]) == S-i:
return False
return True
def Queen(S):
global ans
if S == N: # 끝줄까지 탐색 했으면
ans += 1
else:
for i in range(N):
l[S] = i
if is_promising(S):
Queen(S+1)
N = int(input())
ans = 0
l = [0]*N
Queen(0)
print(ans)5. 후기

- 이 문제.. 백트레킹의 정석 문제라고 불린다. 난 이 문제를 풀며 상당한 고통을 느꼈다. 여러 번의 최적화 끝에 조건문을 간단히 작성하여 is_promising 함수를 완성했다.
백트레킹은 여러 방법이 있는 것 같다. 다른 문제를 풀다 보니
DFS에 백트레킹이 있는 것이 아니라 백트레킹 안에 DFS가 있는 느낌이다.
728x90
반응형
'알고리즘 > python' 카테고리의 다른 글
| [BOJ]ACM Craft(1005), 위상정렬 (0) | 2023.04.19 |
|---|---|
| [BOJ]서강그라운드(14938), 플로이드-워셜 (0) | 2023.04.19 |
| [SWEA] 16940. 퀵 정렬 (0) | 2023.04.19 |
| [BOJ]문자열 게임(18241), 문자열 (0) | 2023.04.19 |
| [BOJ]최소비용 구하기(1916), 다익스트라 (0) | 2023.04.19 |
