위상정렬(Topology)
위상정렬은 순서가 있는 작업을 수행해야 할 때 또는 순서를 결정하는 알고리즘입니다. 즉 노드 간의 선후 관계를 고려하여 정렬하는 알고리즘이라고 할 수 있습니다.
1. 진입차수
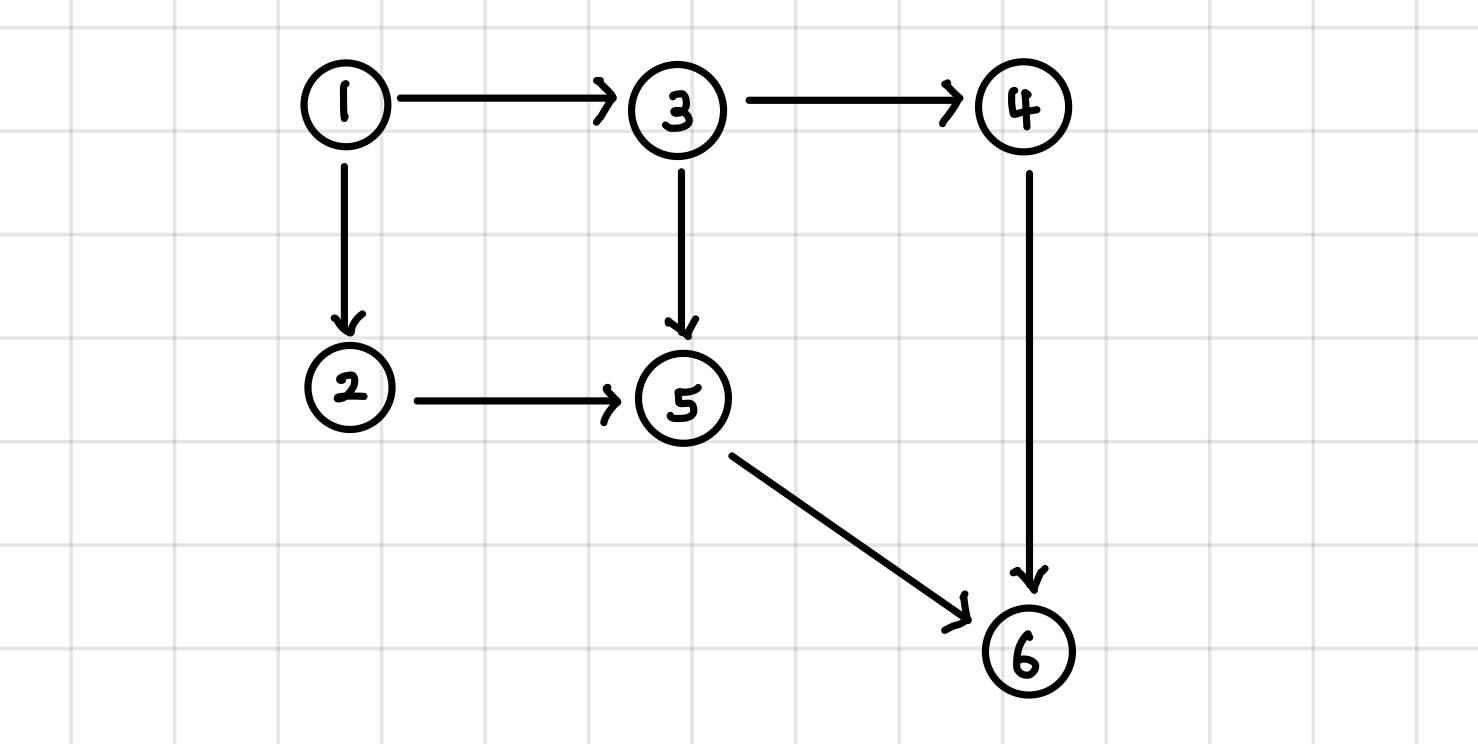
노드 간의 선후 관계를 고려해야 하는 점에서 그래프 알고리즘으로 생각할 수 있다. 선후 관계를 고려한다, 즉 방향성을 거스르지 않도록 순서를 나열하는 방법입니다.
진입차수는 자기 자신으로 연결되어 들어오는 간선의 개수이다.
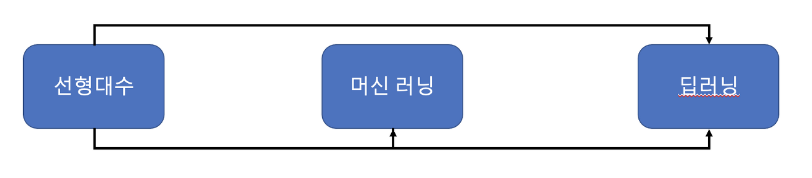
그림에서 보면
- 선형대수 박스의 진입차수는 0,
- 머신러닝 박스의 진입차수는 1,
- 딥러닝 박스의 진입차수는 2
그림을 보면 머신러닝을 수강하려면 선형대수를 우선 수강해야 한다. 또한 머신러닝을 수강하면 딥러닝을 수강할 수 있지만 선형대수만 거쳐도 곧바로 딥러닝을 수강할 수 있다.
2. 위상 정렬
위상 정렬은 진입차수와 큐(que)를 사용합니다.
간단한 단계는 아래와 같습니다.
- 진입차수가 0 인 노드를 큐에 append() 합니다.
- 큐에서 노드를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거합니다.
- 진입차수가 0이 된 노드들을 큐에 넣습니다.
- While Q: 동안 반복합니다.(큐가 빌 때까지)
- 일반적으로 위상 정렬 문제는 사이클이 발생하지 않는다.라는 가정을 두고 시작한다. 만약 위 과정을 거치는 동안 모든 원소를 방문하기 전 즉 큐에서 원소가 전체 노드의 개수만큼 pop() 되지 않았다면 사이클이 존재한다는 것이다. 사이클이 생기면 진입차수가 0이 될 수 없기 때문에 큐에 노드는 들어가지 못한다.
3. 동작과정
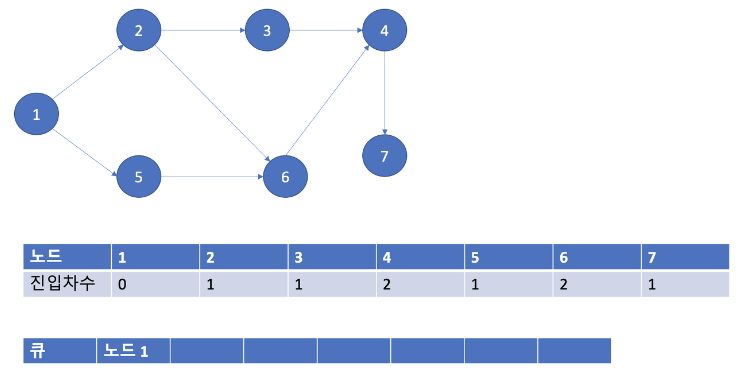
- 노드와 진입차수를 정리합니다. 그리고 노드 1을 큐에 넣습니다.
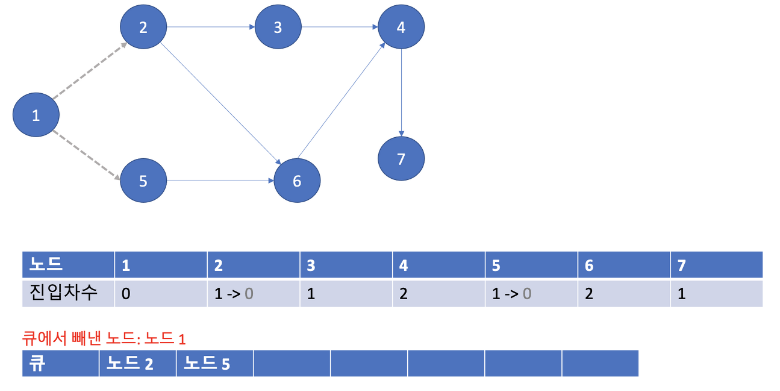
- 노드 1에서 뻗어간 간선을 지워주고 노드 1을 pop() 합니다.
- 진입차수가 0이 된 노드 2와 노드 5를 큐에 append() 합니다.
- 노드 2에서 뻗어간 간선을 지워주고 노드 2를 pop() 합니다.
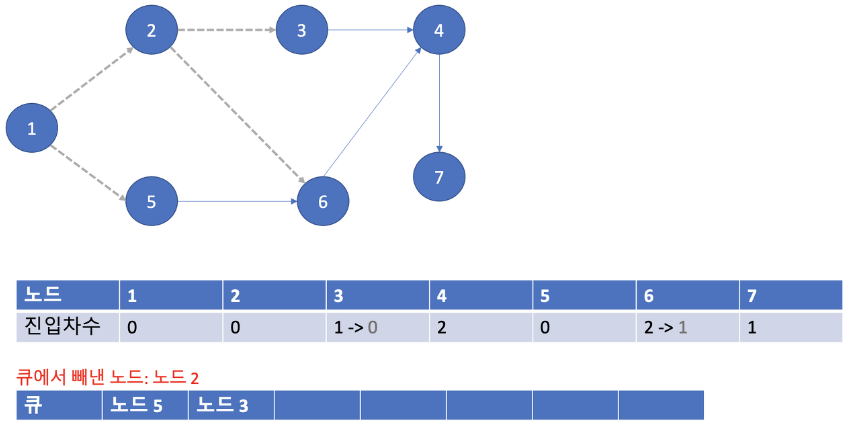
- 진입차수가 0이 된 노드 3을 큐에 append() 합니다.
- 노드 5 에서 뻗어간 간선을 지워주고 노드 5를 pop() 합니다.
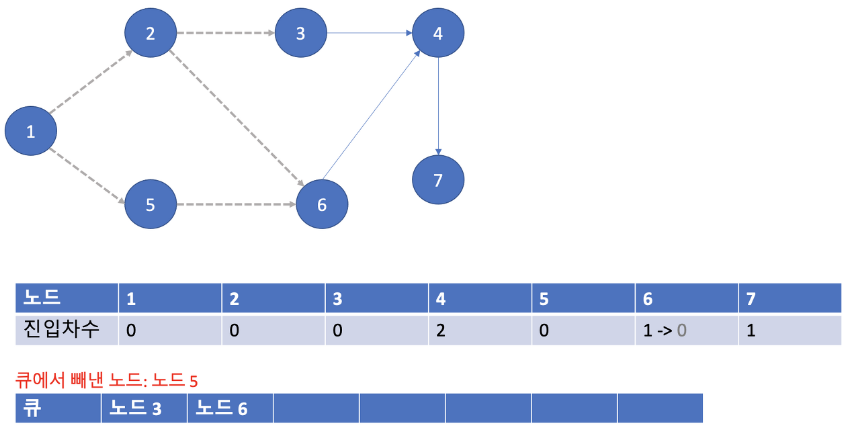
- 진입차수가 0이 된 노드 6를 큐에 append() 합니다.
- 노드 3에서 뻗어간 간선을 지워주고 노드 3을 pop() 합니다.
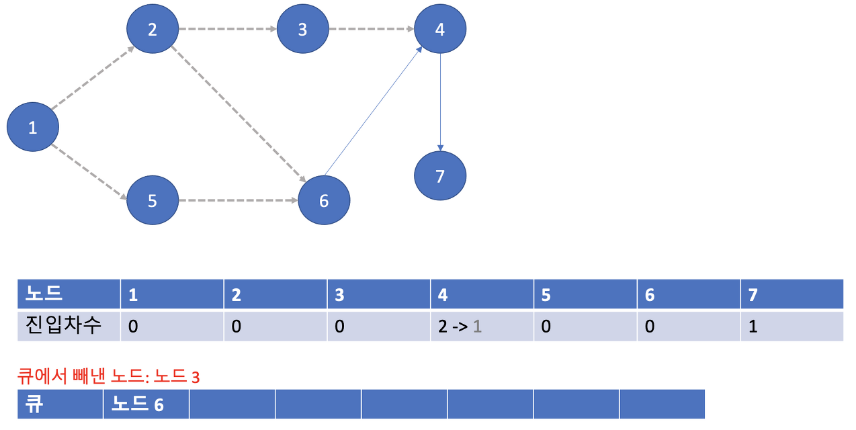
- 진입차수가 0이 된 노드가 없기 때문에 넘어갑니다.
- 노드 6에서 뻗어간 간선을 지워주고 노드 6을 pop() 합니다.
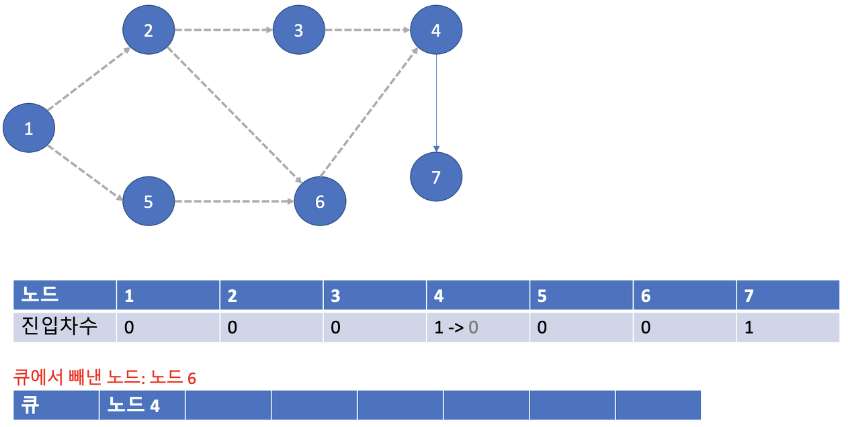
- 진입차수가 0이 된 노드 4를 큐에 append() 합니다.
- 노드 4에서 뻗어간 간선을 지워주고 노드 4를 pop() 합니다.
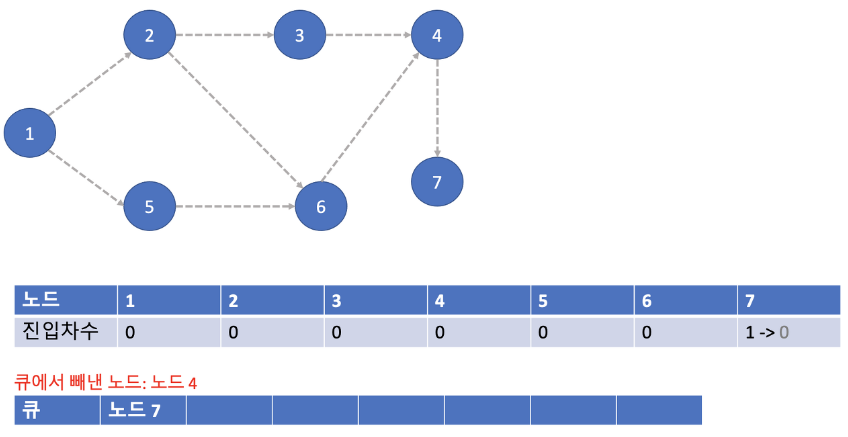
- 진입차수가 0이 된 노드 7을 큐에 append() 합니다.
- 노드 7에서 뻗어간 간선이 없고 남은 노드도 없습니다. 노드 7을 pop() 하게 되면 큐가 비게 되어 종료됩니다.
- 위 과정들을 수행하며 큐에서 pop() 되는 순서대로 출력하면 위상 정렬의 결과가 됩니다.
하지만 위 과정들 중 노드가 2개 이상 들어가는 경우에는 어떤 것이 먼저 들어가냐에 따라 결괏값이 달라질 수 있습니다.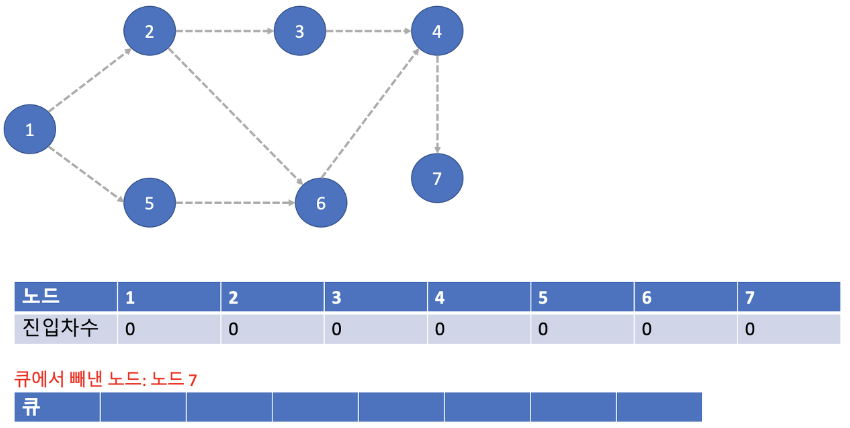
4. 문제 설명
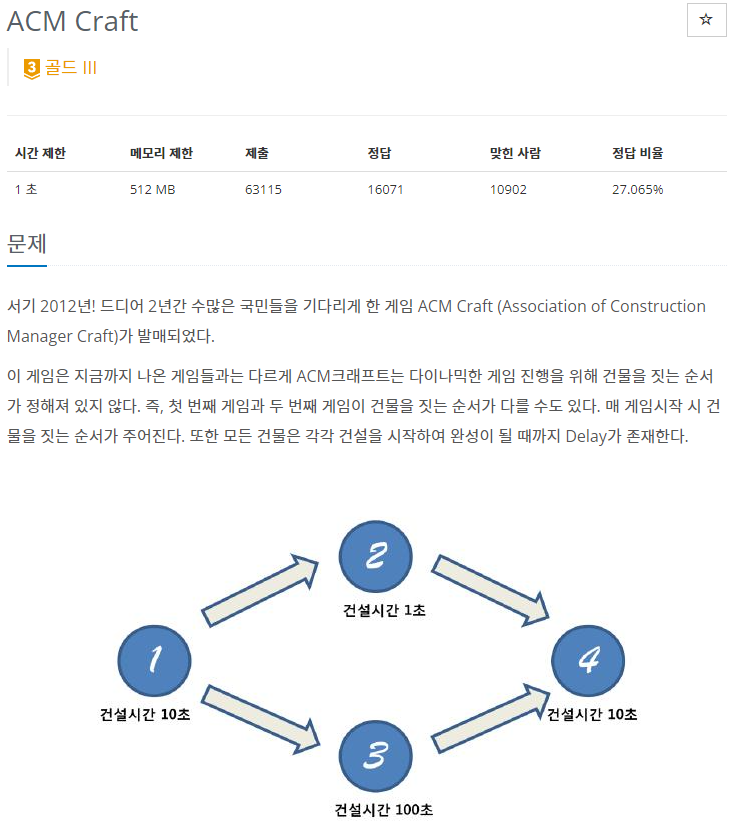

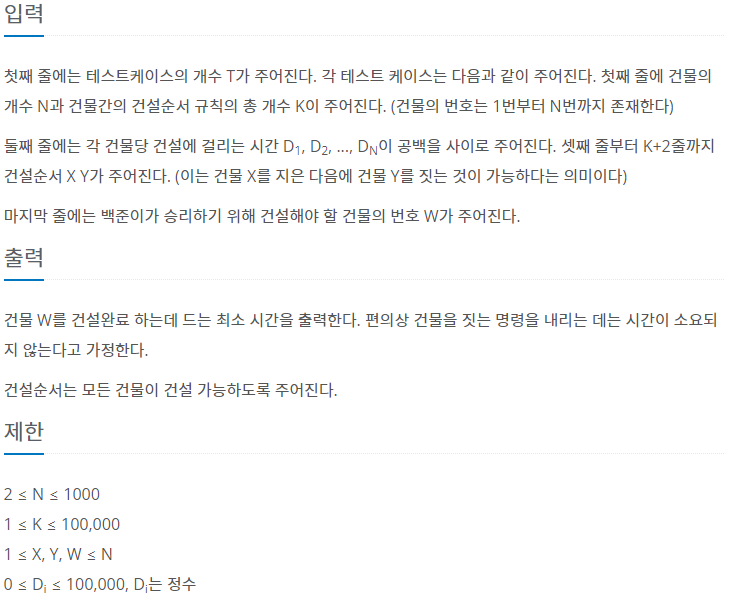
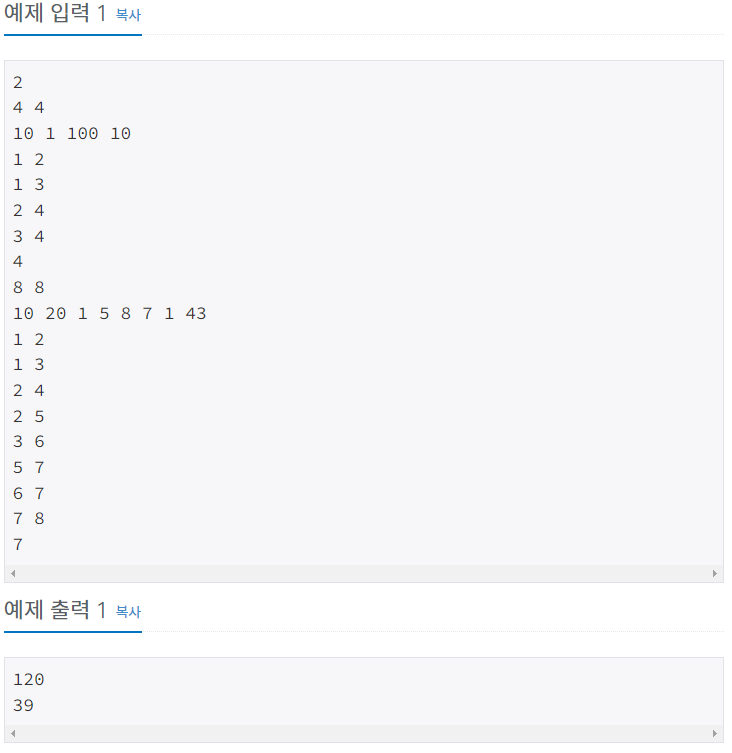
- 문제를 간단히 요약하면 W 번째 건물을 지을 때 걸리는 최소 시간을 계산하는 것이다.
N, K = map(int, input().split())
dev_time = [0] + list(map(int, input().split()))
graph = [[] for _ in range(N+1)]
in_degree = [0] * (N+1)
dp_time = [0] * (N+1)
입력을 받고 빈 list 3개를 만들어 줍시다
- graph는 인접 list를 나타냅니다.
- in_degree는 진입차수를 담는 list입니다.
- dp_time 은 각 건물을 순서에 의해 짓게 될 때 걸리는 최단 시간을 저장하는 list입니다.
# 그래프 만들기, 진입차수 기록하기
def Make_Graph():
for _ in range(K):
a, b = map(int, input().split())
graph[a].append(b)
in_degree[b] += 1
- graph를 작성하고 a -> b 면 b의 진입차수 즉 in_degree [b]의 값이 1개 증가하므로 in_degree도 함께 작성하는 함수를 만듭니다.
# 위상정렬 -> 결과 출력
def Topology():
Q = deque()
for i in range(1, N+1):
if not in_degree[i]:
Q.append(i)
dp_time[i] = dev_time[i]
while Q:
node = Q.popleft()
for next in graph[node]:
in_degree[next] -= 1
dp_time[next] = max(dp_time[node]+dev_time[next], dp_time[next])
if not in_degree[next]:
Q.append(next)
그리고 위상정렬을 해주는 함수를 만듭니다.
1. 먼저 Q를 생성합니다.
2. for문을 이용해서 진입차수가 0인 노드를 Q에 append() 해줍니다.
3. 그리고 Q가 빌 때까지 node에 Q를 하나씩 pop()해서
4. for 문을 통해 간선을 통해 도달한 next(다음노드)마다 그 next의 진입차수를 -1 해주고 건설시간을 초기화해 줍니다.
5. 이 과정에서 진입차수가 0 인 next가 발생했다면** Q에 **append()해줍니다.
Make_Graph() # 그래프 만드는 함수
W = int(input())
Topology() # 위상정렬 과 결과출력
print(dp_time[W])
- W를 받고 dp_time에서 해당 인덱스의 원소를 print 해줍니다.
5. 전체 코드
from collections import deque
# 그래프 만들기, 진입차수 기록하기
def Make_Graph():
for _ in range(K):
a, b = map(int, input().split())
graph[a].append(b)
in_degree[b] += 1
# 위상정렬 -> 결과 출력
def Topology():
Q = deque()
for i in range(1, N+1):
if not in_degree[i]:
Q.append(i)
dp_time[i] = dev_time[i]
while Q:
node = Q.popleft()
for next in graph[node]:
in_degree[next] -= 1
dp_time[next] = max(dp_time[node]+dev_time[next], dp_time[next])
if not in_degree[next]:
Q.append(next)
for _ in range(int(input())):
N, K = map(int, input().split())
dev_time = [0] + list(map(int, input().split()))
graph = [[] for _ in range(N+1)]
in_degree = [0] * (N+1)
dp_time = [0] * (N+1)
Make_Graph() # 그래프 만드는 함수
W = int(input())
Topology() # 위상정렬 과 결과출력
print(dp_time[W])
'알고리즘 > python' 카테고리의 다른 글
| [프로그래머스] lv2 JadenCase 문자열 만들기_python (0) | 2024.03.22 |
|---|---|
| [프로그래머스] lv2 타겟 넘버_python (0) | 2024.03.22 |
| [BOJ]서강그라운드(14938), 플로이드-워셜 (0) | 2023.04.19 |
| [BOJ]N-QUEEN(9663), 백트래킹 (2) | 2023.04.19 |
| [SWEA] 16940. 퀵 정렬 (0) | 2023.04.19 |
위상정렬(Topology)
위상정렬은 순서가 있는 작업을 수행해야 할 때 또는 순서를 결정하는 알고리즘입니다. 즉 노드 간의 선후 관계를 고려하여 정렬하는 알고리즘이라고 할 수 있습니다.

1. 진입차수
노드 간의 선후 관계를 고려해야 하는 점에서 그래프 알고리즘으로 생각할 수 있다. 선후 관계를 고려한다, 즉 방향성을 거스르지 않도록 순서를 나열하는 방법입니다.
진입차수는 자기 자신으로 연결되어 들어오는 간선의 개수이다.

그림에서 보면
- 선형대수 박스의 진입차수는 0,
- 머신러닝 박스의 진입차수는 1,
- 딥러닝 박스의 진입차수는 2
그림을 보면 머신러닝을 수강하려면 선형대수를 우선 수강해야 한다. 또한 머신러닝을 수강하면 딥러닝을 수강할 수 있지만 선형대수만 거쳐도 곧바로 딥러닝을 수강할 수 있다.
2. 위상 정렬
위상 정렬은 진입차수와 큐(que)를 사용합니다.
간단한 단계는 아래와 같습니다.
- 진입차수가 0 인 노드를 큐에 append() 합니다.
- 큐에서 노드를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거합니다.
- 진입차수가 0이 된 노드들을 큐에 넣습니다.
- While Q: 동안 반복합니다.(큐가 빌 때까지)
- 일반적으로 위상 정렬 문제는 사이클이 발생하지 않는다.라는 가정을 두고 시작한다. 만약 위 과정을 거치는 동안 모든 원소를 방문하기 전 즉 큐에서 원소가 전체 노드의 개수만큼 pop() 되지 않았다면 사이클이 존재한다는 것이다. 사이클이 생기면 진입차수가 0이 될 수 없기 때문에 큐에 노드는 들어가지 못한다.
3. 동작과정

- 노드와 진입차수를 정리합니다. 그리고 노드 1을 큐에 넣습니다.

- 노드 1에서 뻗어간 간선을 지워주고 노드 1을 pop() 합니다.
- 진입차수가 0이 된 노드 2와 노드 5를 큐에 append() 합니다.
- 노드 2에서 뻗어간 간선을 지워주고 노드 2를 pop() 합니다.

- 진입차수가 0이 된 노드 3을 큐에 append() 합니다.
- 노드 5 에서 뻗어간 간선을 지워주고 노드 5를 pop() 합니다.

- 진입차수가 0이 된 노드 6를 큐에 append() 합니다.
- 노드 3에서 뻗어간 간선을 지워주고 노드 3을 pop() 합니다.

- 진입차수가 0이 된 노드가 없기 때문에 넘어갑니다.
- 노드 6에서 뻗어간 간선을 지워주고 노드 6을 pop() 합니다.

- 진입차수가 0이 된 노드 4를 큐에 append() 합니다.
- 노드 4에서 뻗어간 간선을 지워주고 노드 4를 pop() 합니다.

- 진입차수가 0이 된 노드 7을 큐에 append() 합니다.
- 노드 7에서 뻗어간 간선이 없고 남은 노드도 없습니다. 노드 7을 pop() 하게 되면 큐가 비게 되어 종료됩니다.
- 위 과정들을 수행하며 큐에서 pop() 되는 순서대로 출력하면 위상 정렬의 결과가 됩니다.
하지만 위 과정들 중 노드가 2개 이상 들어가는 경우에는 어떤 것이 먼저 들어가냐에 따라 결괏값이 달라질 수 있습니다.
4. 문제 설명




- 문제를 간단히 요약하면 W 번째 건물을 지을 때 걸리는 최소 시간을 계산하는 것이다.
N, K = map(int, input().split())
dev_time = [0] + list(map(int, input().split()))
graph = [[] for _ in range(N+1)]
in_degree = [0] * (N+1)
dp_time = [0] * (N+1)
입력을 받고 빈 list 3개를 만들어 줍시다
- graph는 인접 list를 나타냅니다.
- in_degree는 진입차수를 담는 list입니다.
- dp_time 은 각 건물을 순서에 의해 짓게 될 때 걸리는 최단 시간을 저장하는 list입니다.
# 그래프 만들기, 진입차수 기록하기
def Make_Graph():
for _ in range(K):
a, b = map(int, input().split())
graph[a].append(b)
in_degree[b] += 1
- graph를 작성하고 a -> b 면 b의 진입차수 즉 in_degree [b]의 값이 1개 증가하므로 in_degree도 함께 작성하는 함수를 만듭니다.
# 위상정렬 -> 결과 출력
def Topology():
Q = deque()
for i in range(1, N+1):
if not in_degree[i]:
Q.append(i)
dp_time[i] = dev_time[i]
while Q:
node = Q.popleft()
for next in graph[node]:
in_degree[next] -= 1
dp_time[next] = max(dp_time[node]+dev_time[next], dp_time[next])
if not in_degree[next]:
Q.append(next)
그리고 위상정렬을 해주는 함수를 만듭니다.
1. 먼저 Q를 생성합니다.
2. for문을 이용해서 진입차수가 0인 노드를 Q에 append() 해줍니다.
3. 그리고 Q가 빌 때까지 node에 Q를 하나씩 pop()해서
4. for 문을 통해 간선을 통해 도달한 next(다음노드)마다 그 next의 진입차수를 -1 해주고 건설시간을 초기화해 줍니다.
5. 이 과정에서 진입차수가 0 인 next가 발생했다면** Q에 **append()해줍니다.
Make_Graph() # 그래프 만드는 함수
W = int(input())
Topology() # 위상정렬 과 결과출력
print(dp_time[W])
- W를 받고 dp_time에서 해당 인덱스의 원소를 print 해줍니다.
5. 전체 코드
from collections import deque
# 그래프 만들기, 진입차수 기록하기
def Make_Graph():
for _ in range(K):
a, b = map(int, input().split())
graph[a].append(b)
in_degree[b] += 1
# 위상정렬 -> 결과 출력
def Topology():
Q = deque()
for i in range(1, N+1):
if not in_degree[i]:
Q.append(i)
dp_time[i] = dev_time[i]
while Q:
node = Q.popleft()
for next in graph[node]:
in_degree[next] -= 1
dp_time[next] = max(dp_time[node]+dev_time[next], dp_time[next])
if not in_degree[next]:
Q.append(next)
for _ in range(int(input())):
N, K = map(int, input().split())
dev_time = [0] + list(map(int, input().split()))
graph = [[] for _ in range(N+1)]
in_degree = [0] * (N+1)
dp_time = [0] * (N+1)
Make_Graph() # 그래프 만드는 함수
W = int(input())
Topology() # 위상정렬 과 결과출력
print(dp_time[W])
'알고리즘 > python' 카테고리의 다른 글
| [프로그래머스] lv2 JadenCase 문자열 만들기_python (0) | 2024.03.22 |
|---|---|
| [프로그래머스] lv2 타겟 넘버_python (0) | 2024.03.22 |
| [BOJ]서강그라운드(14938), 플로이드-워셜 (0) | 2023.04.19 |
| [BOJ]N-QUEEN(9663), 백트래킹 (2) | 2023.04.19 |
| [SWEA] 16940. 퀵 정렬 (0) | 2023.04.19 |
